Použitie rovníc na vytvorenie priebehov signálu MAUI Studio Pro

Zatiaľ čo generátor signálu v MAUI ® Studio Pro ponúka zjednodušenú metódu simulácie šiestich rôznych priebehov alebo priameho prúdu, jeho skutočná sila spočíva v schopnosti používať rovnice na generovanie ľubovoľných priebehov a tiež aplikovať vlastné vlastnosti kolísania na namerané priebehy signálu.

V nasledujúcom texte vám ukážem príklady bežne používaných priebehov a rovnice, ktoré sú opísané

Prístup k generátoru signálu

K generátoru signálu môžete pristupovať tak, že ho vyberiete z ponuky FILE alebo otvorením karty Generátor signálu v skupine dialógového okna Nastavenie kanála.

Po výbere zdrojového kanála, na ktorom chcete generovať priebeh, vyberte typ priebehu rovnice a aktivujte okno Editor rovníc.

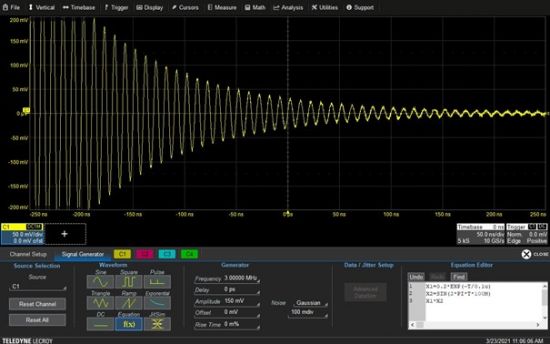
Obrázok 1. - Dialogové okno Generátor signálu zobrazujúci okno Editor rovníc

Nastavenie a rozsah generátora

Pole Generátor v dialogovém okně Generátor signálu řídí amplitudu a svislý posun pro všechny průběhy vytvořené pomocí rovnic. Všimněte si, že generátor signálu změní velikost amplitudy rovnice na vybraný rozsah amplitudy.

Funkcie a prevádzkovatelia

Generátor signálu podporuje jedenásť matematických funkcií a deväť operátorov, stručne popísaných nižšie. Umožňuje tiež použitie premenných, pevných argumentov a konštant v rámci rovníc.

Funkcia

• ABS (  )  Absolútna hodnota, vypočíta absolútnu hodnotu, unipolárnu veľkosť funkcie alebo argumentu;
• COS ( )   Cosine, vypočíta cosine argumentu;
• EXP (  )  Exponenciálne, vypočíta exponenciálne pomocou základne prirodzených logaritmov; 
• FLOOR ( ) Prahová hodnota, vypočíta sa celá hodnota funkcie;;
• LN ( ) Prirodzený logaritmus, výpočet prirodzeného logaritmu, základ e argumentu alebo funkcie;
• LOG  ( )  Logaritmus, vypočíta logaritmus zo základu 10, argumentu alebo funkcie; 
• PULSE ( ) Vytvára pulznú jednotku pomocou umiestnenia hradiel alebo funkcií určených v argumente;  
• SIN  (  ) Sin, vypočíta sinus argumentu;
• SQRT ( ) Odmocnina z druhej mocniny vypočíta odmocninu z argumentu alebo funkcie;
• KROK (  ) Krok, vytvára krok jednotky v mieste určenom argumentom alebo funkciou;
• TAN (  )  Tangens, vypočíta tangens argumentu;

Operátory

• + Sčítanie
• - Odčítanie
• * Násobenie
• / Delenie
• ↑ Umocnenie
• = Rovnať sa

( ) Matematické zoskupenie

• , Čiara, oddeľovač argumentov

Premenná

Premenné X1 až x16, za ktorými nasleduje symbol, sa môžu použiť na označenie obsahu ľubovoľného riadku v Editore rovniciach. Opis premennej sa potom môže použiť na nahradenie obsahu v inej rovnici.

Pro rovnicu:

X1=SIN(2*PI*10E6*T)

X2=(1+0,75*COS(2*PI*1E3*T))

X1*X2

Produkt X1 * X2 sa vypočíta takto​:

SIN(2*PI*10E6*T)*(1+0,75*COS(2*PI*1E3*T))

Poznámka:

Vypočíta sa len konečný riadok každej rovnice; všetky ostatné riadky, ktoré nie sú definované ako premenné, sa ignorujú. Preto by sa mali rovnice, ktoré obsahujú viac riadkov, rozdeliť do jedného riadku, pričom konečný riadok počíta premenné, ako je uvedené vyššie.

Vo všeobecnosti možno rovnice vymyslieť ako jednu funkciu na riadok / premennú, s výnimkou funkcie Pulse. Vzhľadom na to, že funguje ako funkcia / multiplikátor, je najlepšie ju zachovať na rovnakom riadku ako ostatné výrazy, na ktorých pracuje..

Argument:

Na použitie v rovniciach je k dispozícii päť funkčných argumentov:

• 2 * PI * T Fázová premenná pre trigonometrické funkcie v radiálnych sekundách ; 
• T časová premenná v sekundách;
• PI Číselná konštanta 3.14159265358979;
• NOISE rovnomerne rozložené náhodné čísla 0-1, priemer = 0,5, štandardná odchýlka = 0,288;
• GNOISE Gaussian distribuoval náhodné čísla 0 – 1, priemer = 0,5, štandardná odchýlka = 0,1667;

Multiplikátory:

Štandardné multiplikátory podporujú: p (pico, 1E-12); n (nano, 1E-9); μ nebo u (mikro, 1E-6); m (milli, 1E-3); k (kilo, 1E3); M (Mega, 1E6).

Pri zadávaní priebehu sa musí uviesť len násobok (ak je to relevantné) a hodnota; predpokladá sa merná jednotka pre každú funkciu a argument.

Rovnica

Na nasledujúcich stranách obsahuje každý typ priebehov všeobecnú rovnicu zobrazujúcu funkcie, konštanty, argumenty a premenné použité na vytvorenie tohto Tvaru signálu. Konštanty zadané užívateľom sú opísané všeobecne.

K tomu je priložená príklad rovnice, ktorá by vytvorila priebeh znázornený na obrázku za predpokladu vertikálneho nastavenia stupnice kanála 500 mV / delenie, horizontálneho nastavenia stupnice 1 μs / delenie so spomalením – 5 μs a nastavenia amplitúdy generátora signálu 1 V. Táto názorná rovnica môže byť vložená do Editoru rovníc tak, ako je, alebo upravená podľa požadovanej mierky.

Obrázok		Názov	Príklad
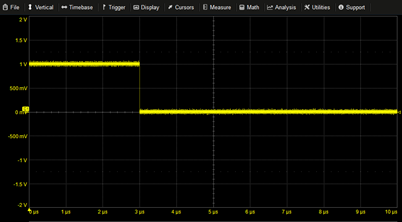		Time Reversed Unit Step	Step(3u-T)
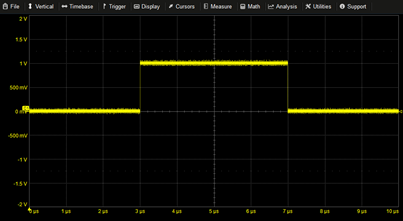		Unit Pulse	PULSE(3u,7u)
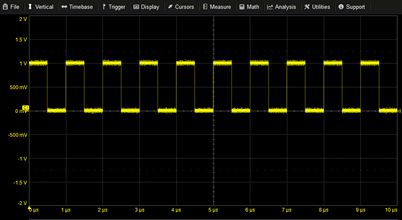		Pulse Train	STEP(SIN(2*PI*T*1M))
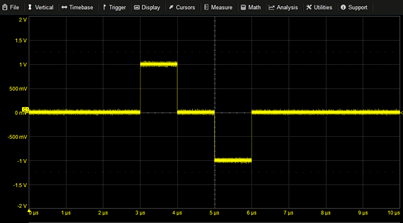		Tri-level Pulse	PULSE(3u,4u)-PULSE(5u,6u)
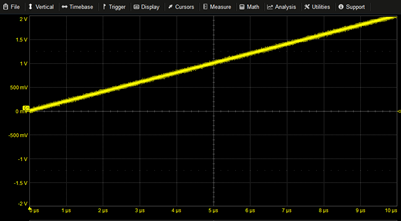		Ramp	0.2M*T
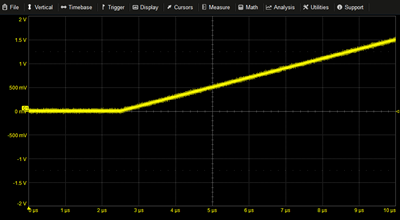		Delayed Ramp	0.2M*(T-2.5u)*STEP(T-2.5u)
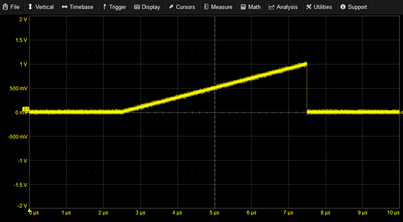		Truncated Ramp	0.2M*(T-2.5µ)*PULSE(2.5µ,7.5µ)
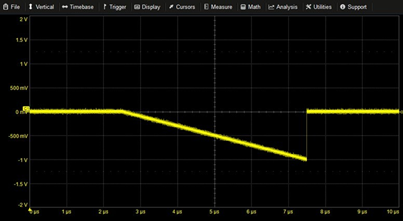		Truncated Negative Ramp	-0.2M*(T-2.5µ)*PULSE(2.5µ,7.5µ)
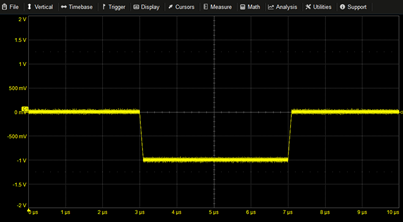		Trapezoidal Pulse with Adjustable Transition Times	X1=-10M*(T-3µ)*STEP(T-3µ) X2=10M*(T-3.1µ)*STEP(T-3.1µ) X3=10M*(T-7µ)*STEP(T-7µ) X4=-10M*(T-7.1µ)*STEP(T-7.1µ) X1+X2+X3+X4
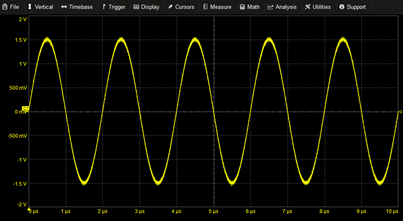		Sine	1.5*SIN(2*PI*T*0.5M)
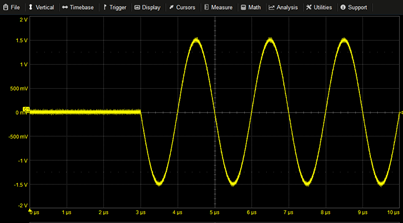		Gated Sine	1.5*SIN(2*PI*T*0.5M)*STEP(T-3µ)
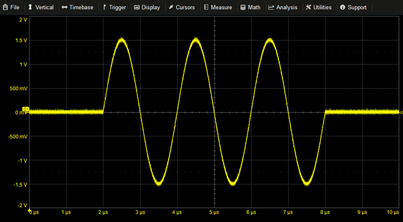		Sine Burst	1.5*SIN(2*PI*T*0.5M)*PULSE(2µ,8µ)
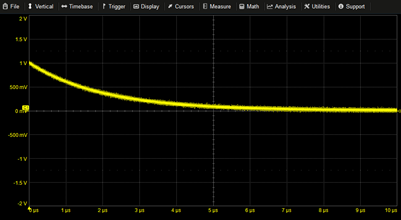		Decaying Exponential	EXP(-T/2µ)
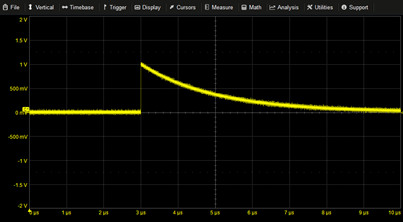		Delayed Exponential Decay	EXP(-(T-3µ)/2µ)*STEP(T-3µ)
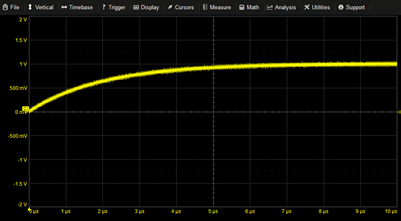		Rising Exponential	1-EXP(-T/2µ)
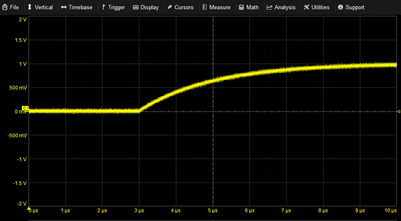		Delayed Rising Exponential	(1-EXP(-(T-3µ)/2µ))*STEP(T-3µ)
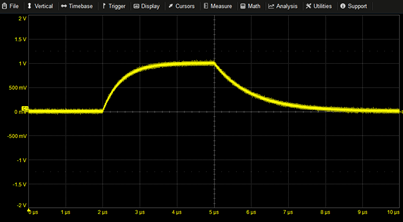		Exponential Pulse with Different Rise/Fall Constants	X1=(1-EXP(-(T-2µ)/0.5µ))*PULSE(2µ,5µ) X2=(EXP(-(T-5µ)/1µ)*STEP(T-5.0001µ)) X1+X2
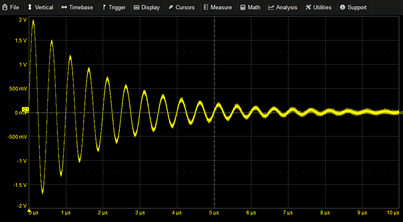		Exponentially Damped Sine	2*EXP(-T/2µ)*SIN(2*PI*T*2M)
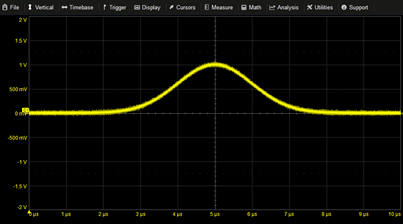		Gaussian Pulse	EXP(-(1/2)*((T-5µ)/1µ)^2)
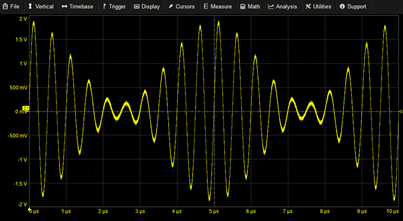		Amplitude Modulation	X1=SIN(2*PI*T*2M) X2=(1+0.85*COS(2*PI*T*0.2M)) X1*X2
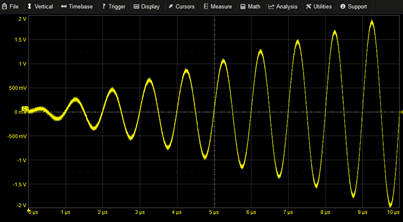		Sine Amplitude Sweep	0.2M*T*SIN(2*PI*T*1M)
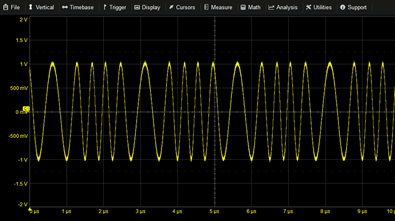		Frequency Modulation	SIN(2*PI*T*2M+2*COS(2*PI*T*0.4M))
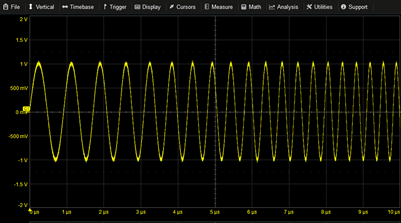		Linear Frequency Sweep	SIN(PI*(2*T*1M+((4M-1M)/10µ)*T^2))
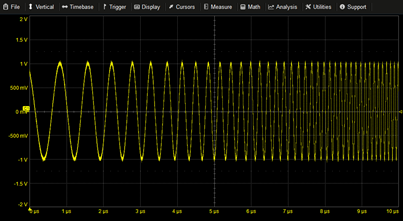		Logarithmic Frequency Sweep	X1=LN(10M/1M)/10µ SIN(2*PI*((1M/X1)*(EXP(X1*T)-1)))
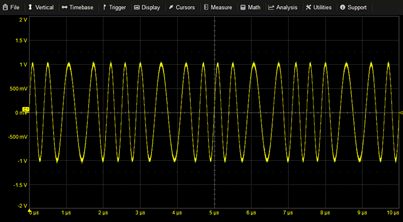		Phase Modulation	SIN(2*PI*T*2M+PI/2*SIN(2*PI*T*0.4M))
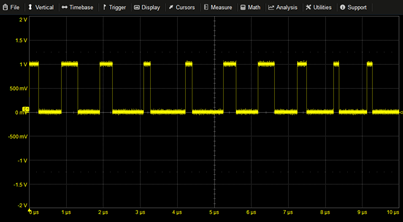		Pulse Width Modulation	X1=SIN(2*PI*T*1M+PI/2*COS(2*PI*T*0.1M)) X2=SIN(2*PI*T*1M+PI/2*SIN(2*PI*T*0.1M)) STEP(X1)*STEP(X2)
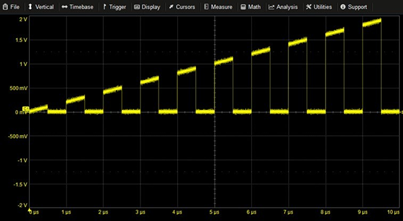		Pulse Amplitude Modulation	0.2M*T*STEP(SIN(2*PI*T*1M))
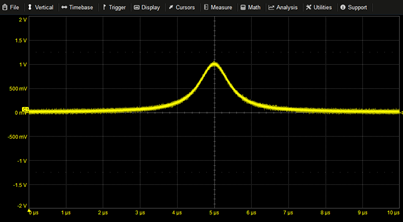		Lorentz Pulse	1/(1+((T-5µ)/0.5µ)^2)
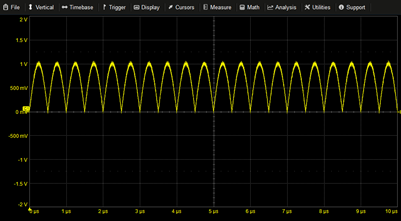		Full Wave Rectified Sine	ABS(SIN(2*PI*T*1M))
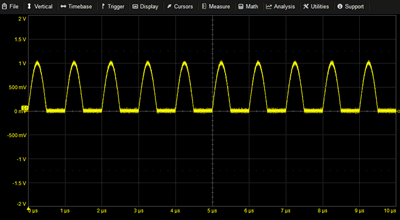		Half Wave Rectified Sine	X1=SIN(2*PI*T*1M) X2=STEP(X1) X1*X2
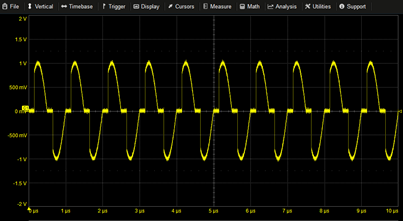		Gated Sine-variable Duty Cycle	X1=0.15µ X2=SIN(2*PI*T*1M) X3=SIN(2*PI*(T-X1)*1M) STEP(X2*X3)*X2
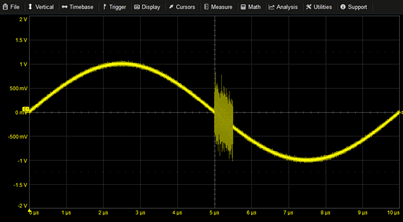		Additive Noise Burst	X1=SIN(2*PI*T*100k) X2=(NOISE-0.5) *PULSE(5µ,5.5µ) X1+X2

Tento softvér si môžete vyskúšať zadarmo. Stačí, že sa na nás obráťte s formulárom.

Sme vám úplne k dispozícii a v prípade záujmu vás ukážem krok za krokom, kde softvér zohýbať a ako s ním ďalej pracovať.

Maui Studio / Softwarová dedičnosť / Remote Control / Priebeh signálov z osciloskopov iných výrobcov

Osciloskopy Teledyne LeCroy HDO6000B a HDO6000B-MS

Digitálne osciloskopy s rozlíšením 12 bitov, šírkou pásma 350 MHz do 1 GHz, pamäťou až 250 MS na kanál, vzorkovaním 10 GSa.

Osciloskop Teledyne LeCroy HDO 9000

Veľmi rýchle štviorkanálové digitálne osciloskopy radu HDO 9000 so šírkou pásma 1 GHz až 4 GHz, pamäťou až 128 Mpts na kanál a rýchlosťou vzorkovania až 40 GS/s. Poskytujú výnimočnú vernosť signálu s 10-bitovým rozlíšením.

12-bitové osciloskopy Teledyne LeCroy HDO4000 a HDO4000-MS

12-bitové štvorkanálové a dvojkanálové digitálne osciloskopy Teledyne LeCroy so šírkou pásma 200 MHz až 1 GHz, pamäťou až 50 M na kanál, vzorkovaním 2,5 GSa/s a možnosťou rozšírenia o interný 16-kanálový logický analyzátor.

Osciloskopy radu Teledyne LeCroy HDO8000

Osemkanálové osciloskopy Teledyne LeCroy radu HDO8000 so šírkou pásma od 350 MHz do 1 GHz s dvanásťbitovými AD prevodníkmi pracujúcimi na frekvencii 2,5 GHz.